Use seaduck.Particle with AVISO#
Particles are simulated in the Southern Ocean AVISO altimetry surface-ocean velocity field.
Author: Wenrui Jiang, Tom Haine Feb ‘23
Show code cell source
import cartopy.crs as ccrs
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import seaduck as sd
mpl.rcParams["figure.dpi"] = 300
Loading data#
The velocity field dataset is derived from AVISO sea surface height products, which were processed by SSALTO/DUACS and distributed by AVISO+ (https://www.aviso.altimetry.fr) with support from CNESThose products were processed by SSALTO/DUACS and distributed by AVISO+ (https://www.aviso.altimetry.fr) with support from CNES. The velocities are defined on a lat-lon grid with staggered velocity components. It’s a snapshot from a single time (see below). seaduck.utils provides a few datasets for testing and demonstration purposes. The corresponding dataset is called when the corresponding functions are called.
ds = sd.utils.get_dataset("aviso")
ds
<xarray.Dataset> Size: 4MB
Dimensions: (Y: 300, X: 3600, Yp1: 300, Xp1: 3600, time: 1)
Coordinates:
* Y (Y) float32 1kB -74.9 -74.8 -74.7 -74.6 ... -45.3 -45.2 -45.1 -45.0
* X (X) float32 14kB -179.9 -179.8 -179.7 -179.6 ... 179.8 179.9 180.0
* Yp1 (Yp1) float32 1kB -74.95 -74.85 -74.75 ... -45.25 -45.15 -45.05
* Xp1 (Xp1) float32 14kB -179.9 -179.9 -179.8 ... 179.8 179.9 179.9
* time (time) datetime64[ns] 8B 2017-01-01
Data variables:
lat (Y) float32 1kB dask.array<chunksize=(300,), meta=np.ndarray>
lon (X) float32 14kB dask.array<chunksize=(3600,), meta=np.ndarray>
u (Yp1, X) float16 2MB dask.array<chunksize=(75, 1800), meta=np.ndarray>
v (Y, Xp1) float16 2MB dask.array<chunksize=(75, 1800), meta=np.ndarray>
Attributes: (12/42)
Conventions: CF-1.6
Metadata_Conventions: Unidata Dataset Discovery v1.0
cdm_data_type: Grid
comment: Sea Surface Height measured by Altimetry...
contact: aviso@altimetry.fr
creator_email: aviso@altimetry.fr
... ...
summary: CLS Delayed-Time Level-4 sea surface hei...
time_coverage_duration: P1D
time_coverage_end: 2017-01-01T12:00:00Z
time_coverage_resolution: P1D
time_coverage_start: 2016-12-31T12:00:00Z
title: DT merged all satellites Global Gridded ...Now, create the OceData object which provides methods to translate between lat-lon and grid-oriented coords. The model coords frequently needed are also cached.
bathtub = sd.OceData(ds)
The object also contains a tp (topology) object. It looks at the shape of the coordinate data. In this Southern Ocean case, based on the longitude range, it thinks the type is x_periodic, which is correct for the Southern Ocean.
bathtub.tp.typ
'x_periodic'
We’ve prepared the bathtub that the ducks are going to swim (passively drift) in. Now decide where and when to drop them.
We are going to use a short-hand defined in seaduck.utils to define the initial position for simplicity. The returns are normally four 1D numpy array of lon, lat, dep, and time. It’s as simple as that.
# Define the extend of the box
west = -180.0
east = 180.0
south = -74.99
north = -40.01
shallow = -10.0
deep = -10.0
time = "1970-01-01"
Nlon = 300 # How many along longitudinal direction?
Nlat = 30 # How many along latitudinal direction?
Ndep = 1 # How many along vertical direction?
x, y, z, t = sd.utils.easy_3d_cube(
(west, east, Nlon),
(south, north, Nlat),
(shallow, deep, Ndep),
time,
print_total_number=True,
)
A total of 9000 positions are defined.
Here is where the particles start on the map:
Show code cell source
plt.figure(figsize=(16, 9))
ax = plt.axes(projection=ccrs.SouthPolarStereo(central_longitude=170.0))
ax.plot(x, y, "r+", markersize=1, transform=ccrs.PlateCarree())
ax.coastlines()
ax.set_title("Particle initial position")
plt.show()
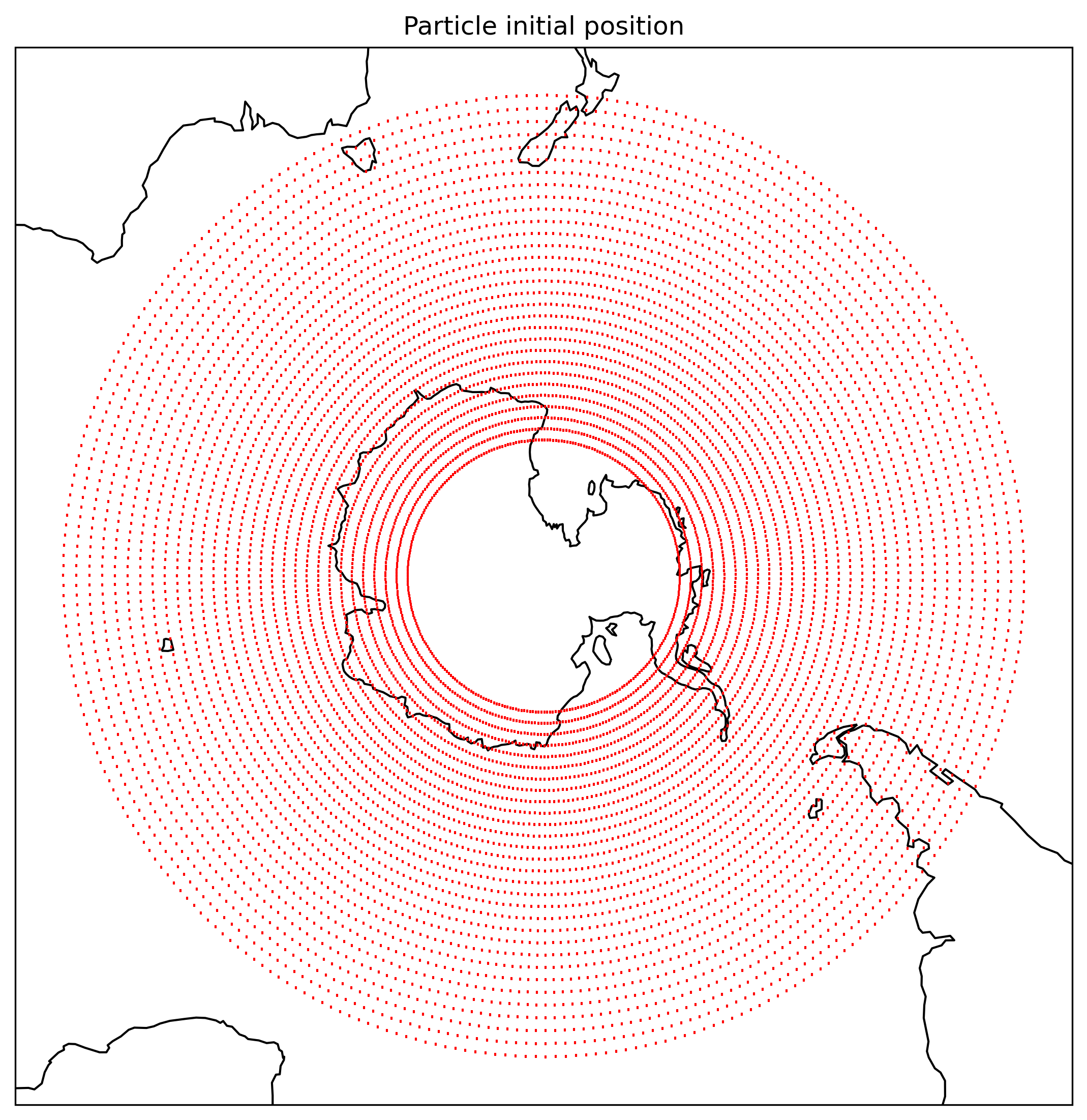
Fig.1 Initial position of the particles.
The AVISO velocity data only has the horizontal velocity component. Or in other words, all the particles are assumed to be at the same (implicit) level, which is the surface for this example. seaduck takes care of that by just setting:
z = None
The AVISO velocity field is a snapshot and does not have a time dimension. Therefore, the time is only valid in a relative sense, i.e. how long has the simulation gone in “real” time.
The standard format for time in seaduck is seconds since 1970-01-01 00:00, and it could be negative. Remember what time is set as the initial time?
all(t == 0)
True
Let’s now define the duration of the simulation (end before start means integrate backwards in time). We can again use a short hand from seaduck.utils.
tf = sd.utils.convert_time("1970-02-01")
This is equivalent to:
We’re not interested when particles leave the domain, so we disregard the ones that leave from the northern boundary by defining:
def interested_in(p):
return np.logical_and(-74.5 < p.lat, p.lat < -45.5)
Create the OceInterp.lagrangian.particle object.#
We have all the information we need. The final step of preparation is to create the seaduck.lagrangian.particle object. We need to tell the seaduck this information about the particles: where and when they start, which bathtub they’re in, and the names of the velocity components; because it’s not great at guessing.
p = sd.Particle(
x=x,
y=y,
z=z,
t=t,
data=bathtub,
uname="u",
vname="v",
wname=None,
callback=interested_in,
)
p
<seaduck.lagrangian.Particle at 0x7ff62c321650>
Perform the particle trajectory simulation.#
The to_list_of_time method does the Lagrangian trajectory calculation.
Notice how we define when to dump output (normal_stops) and when to update the velocity field (update_stops). By default, the stops returned by the integration is the combination (union) of normal_stops and update_stops. raw is a list of OceInterp.eulerian.position objects with the same length as stops.
normal_stops = np.linspace(t[0], tf, 10)
stops, raw = p.to_list_of_time(normal_stops=normal_stops)
1970-01-01T00:00:00
1970-01-04T10:40:00
1970-01-07T21:20:00
1970-01-11T08:00:00
1970-01-14T18:40:00
1970-01-18T05:20:00
1970-01-21T16:00:00
1970-01-25T02:40:00
1970-01-28T13:20:00
1970-02-01T00:00:00
Plotting#
First we extract the longitude and latitude from the raw object.
lons = np.array([pt.lon for pt in raw]).T
lats = np.array([pt.lat for pt in raw]).T
Some particles passed through the dateline (periodic boundary). Here is some post-processing to handle the plot.
Show code cell source
for i in range(len(lons)):
diff = np.diff(lons[i])
if max(abs(diff)) > 330:
for j in np.where(abs(diff) > 300)[0]:
j = int(j)
lons[i, j + 1 :] -= np.sign(diff[j]) * 360
Voila!
Show code cell source
plt.figure(figsize=(9, 16))
ax = plt.axes(projection=ccrs.SouthPolarStereo(central_longitude=170.0))
ax.plot(lons.T, lats.T, "darkblue", lw=0.3, transform=ccrs.PlateCarree())
ax.coastlines()
ax.set_title("Particle trajectories")
plt.show()
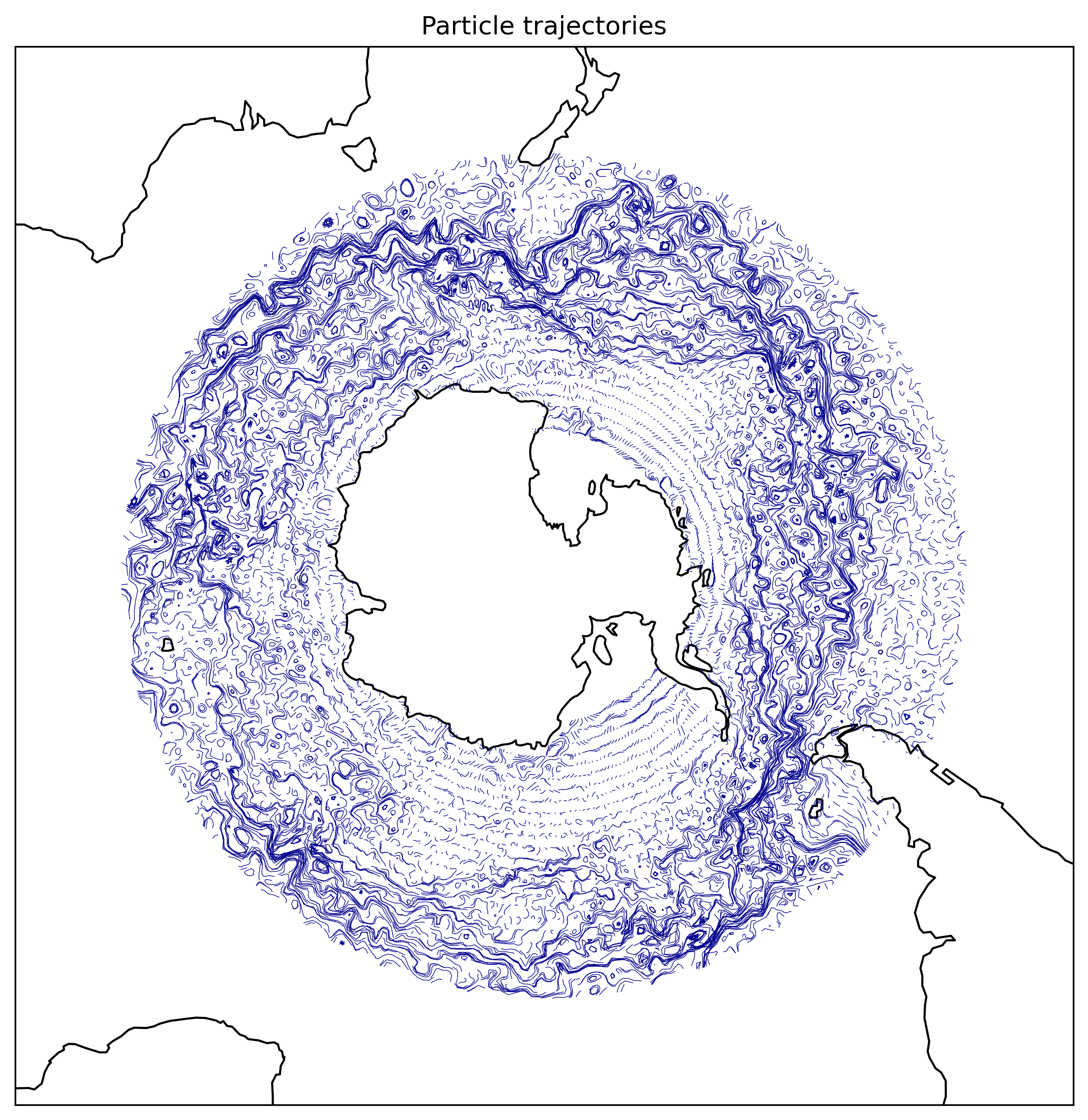
Fig.2 The trajectories of particles advected by AVISO-derived surface velocity field.
Advanced use of Particle#
In this subsection, we are going to demonstrate how to access the analytical trajectories of particles. We are also going to demonstrate the flexibility of Particle release.
Most of the notebooks release particles at the same time. We are going to do it differently this time. They are going to be released at 64W and 55S and 64S. Crucially, all of the particles are released at a different time.
Show code cell source
N = 777
t_earliest = sd.utils.convert_time("1970-01-01")
t_final = sd.utils.convert_time("1970-02-01")
t_latest = sd.utils.convert_time("1970-03-03") # damn you, February.
t = np.linspace(t_earliest, t_latest, N)
number_of_loop = 6.18
# y = -65.0+np.abs(10-np.linspace(0,number_of_loop*20,N)%20)
y = -59.5 + 4.5 * np.sin(number_of_loop * np.linspace(-3.14, 3.14, N))
x = np.ones(N) * (-64.0)
z = -np.ones(N)
To better demonstrate, here is a plot showing the release pattern of the particle. The time is referenced against the final time of the simulation. Note that every single particle will be released at a different time and there are going to be both forward and backward particles in the same simulation.
This is as if there is a ship is commuting in drake passage while releasing particles.
Show code cell source
plt.plot(t, y, "o", markersize=1)
plt.xticks(
[t_earliest, t_final - 15 * 86400, t_final, t_final + 15 * 86400, t_latest],
["-31 days", "-15 days", "0", "+15 days", "+31 days"],
)
plt.ylabel("Latitude")
plt.title("Latitude of particles released at 64W")
plt.show()
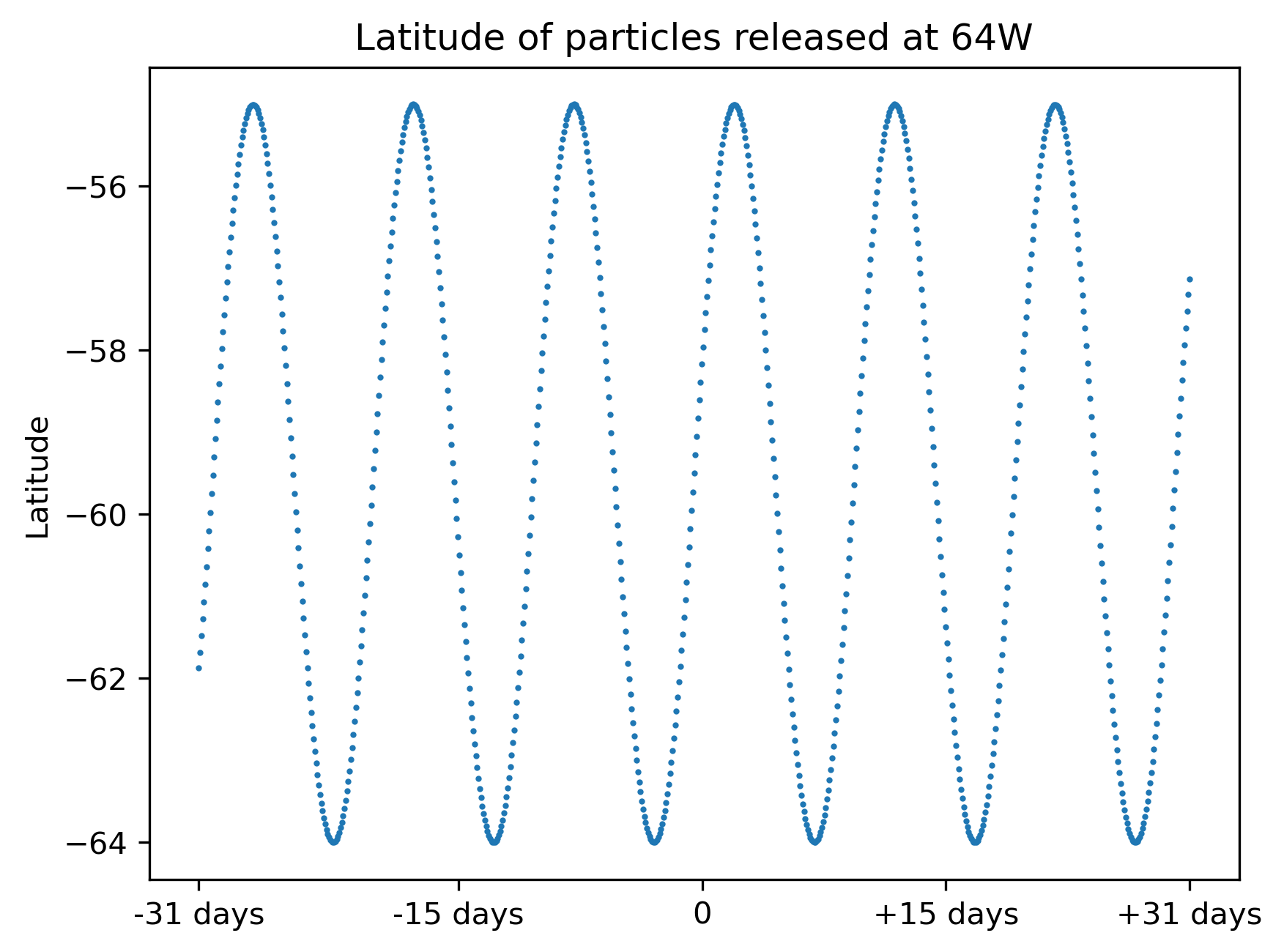
Fig.3 Pattern of particle release. Time is relative to the final time.
The only difference in preparation between this one and the previous simulation is that we have save_raw = True. This means the particles will record all the necessary informations to reconstruct the analytical trajectory.
p = sd.Particle(
x=x,
y=y,
z=z,
t=t,
data=bathtub,
uname="u",
vname="v",
wname=None,
callback=interested_in,
save_raw=True,
)
No tricks need to be played while execution.
%%time
p.to_next_stop(t_final)
CPU times: user 1.25 s, sys: 24 ms, total: 1.28 s
Wall time: 1.27 s
When save_raw = True is selected, the Particle object records location and velocity information everytime velocity is updated. The following plot is plotted from longitude and latitudes of particles crossing cell walls. Each trajectory is colored based on the time of release, Purple is the earliest, red is the latest (furthest into the future).
Show code cell source
plt.figure(figsize=(9, 16))
ax = plt.axes(projection=ccrs.PlateCarree())
rainbow = plt.get_cmap("rainbow")
for i in range(0, N):
color = rainbow(t[i] / 2 / t_final)
ax.plot([x[i]] + p.xxlist[i], [y[i]] + p.yylist[i], color=color, lw=0.2)
ax.coastlines()
plt.show()
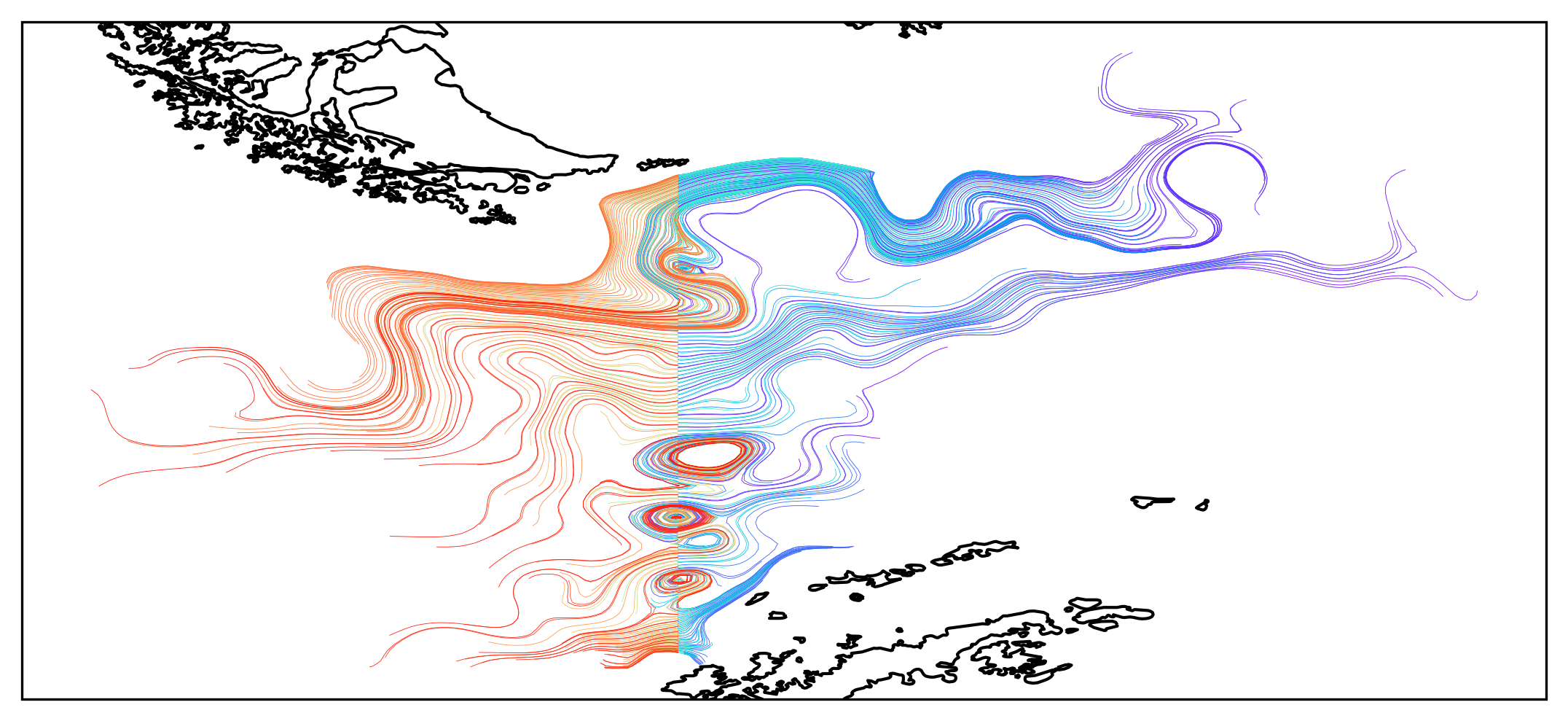
Fig.4 Trajectory of particles released at different time. Warm color are particles released after the final time, and cold colors are those released before the final time.
