Vertical stream function conservation#
author, Wenrui Jiang 06/06/2022
This notebook is also an idealized test for 2D flow like the horizontal case. However, it has a slightly different flavor.
This notebook looks at the vertical direction rather than the horizontal one.
We are going to simulate the particles backward in time.
The “wall” behavior of the particles are explored.
Show code cell source
import warnings
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import xarray as xr
from matplotlib import cm, colors
import seaduck as sd
mpl.rcParams["figure.dpi"] = 300
warnings.filterwarnings("ignore")
Loading data#
As always, we need to load the data. For simplicity and to demonstrate the capacity of particles sliding on the wall, I am going to use the stream function of an \(f\)-plane gyre. You can think of this example as a zonal overturning cell in a meridional channel.
def streamfunction(x, z):
tempz = -z / 500 - 1
return np.cos(np.pi * x / 2) * np.cos(np.pi * tempz / 2)
Show code cell source
N = 100
M = 50
x = np.linspace(-1, 1, N + 1)
y = np.linspace(-0.1, 0.1, 2)
zl = np.linspace(0, -1000, M)
zp1 = np.append(zl, -1001)
xg, yg = np.meshgrid(x, y)
xv = 0.5 * (xg[:, 1:] + xg[:, :-1])
yv = 0.5 * (yg[:, 1:] + yg[:, :-1])
xu = 0.5 * (xg[1:] + xg[:-1])
yu = 0.5 * (yg[1:] + yg[:-1])
xc = 0.5 * (xv[1:] + xv[:-1])
yc = 0.5 * (yv[1:] + yv[:-1])
tempx, tempz = np.meshgrid(x, zl)
strmf = streamfunction(tempx, tempz).reshape(len(zl), 1, -1)
z = 0.5 * (zp1[1:] + zp1[:-1])
zl = zp1[:-1]
drf = np.abs(np.diff(zp1))
u = np.zeros((M, 1, N + 1), float)
u[:-1] = np.diff(strmf, axis=0)
w = np.diff(strmf, axis=-1)
v = np.zeros((M, 2, N), float)
Show code cell source
stream = np.zeros((M, 2, N + 1))
stream[:] = strmf
Show code cell source
ds = xr.Dataset(
coords=dict(
XC=(["Y", "X"], xc),
YC=(["Y", "X"], yc),
XG=(["Yp1", "Xp1"], xg),
YG=(["Yp1", "Xp1"], yg),
Zl=(["Zl"], zl),
Z=(["Z"], z),
drF=(["Z"], drf),
rA=(["Y", "X"], np.ones_like(xc, float)),
),
data_vars=dict(
UVELMASS=(["Z", "Y", "Xp1"], u),
VVELMASS=(["Z", "Yp1", "X"], v),
WVELMASS=(["Zl", "Y", "X"], w),
streamfunc=(["Zl", "Yp1", "Xp1"], stream),
),
)
ds
<xarray.Dataset> Size: 248kB
Dimensions: (Z: 50, Y: 1, Xp1: 101, Yp1: 2, X: 100, Zl: 50)
Coordinates:
XC (Y, X) float64 800B -0.99 -0.97 -0.95 -0.93 ... 0.95 0.97 0.99
YC (Y, X) float64 800B 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0
XG (Yp1, Xp1) float64 2kB -1.0 -0.98 -0.96 -0.94 ... 0.96 0.98 1.0
YG (Yp1, Xp1) float64 2kB -0.1 -0.1 -0.1 -0.1 ... 0.1 0.1 0.1 0.1
* Zl (Zl) float64 400B 0.0 -20.41 -40.82 ... -959.2 -979.6 -1e+03
* Z (Z) float64 400B -10.2 -30.61 -51.02 ... -969.4 -989.8 -1e+03
drF (Z) float64 400B 20.41 20.41 20.41 20.41 ... 20.41 20.41 1.0
rA (Y, X) float64 800B 1.0 1.0 1.0 1.0 1.0 ... 1.0 1.0 1.0 1.0 1.0
Dimensions without coordinates: Y, Xp1, Yp1, X
Data variables:
UVELMASS (Z, Y, Xp1) float64 40kB 3.923e-18 0.002012 0.004023 ... 0.0 0.0
VVELMASS (Z, Yp1, X) float64 80kB 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0
WVELMASS (Zl, Y, X) float64 40kB 1.923e-18 1.921e-18 ... -1.923e-18
streamfunc (Zl, Yp1, Xp1) float64 81kB 3.749e-33 1.923e-18 ... 3.749e-33Prepare the test#
First, we convert the xarray.Dataset to seaduck.OceData
tub = sd.OceData(ds)
Now we define the initial condition of particles such that some particles are right on the wall/at the corner.
n = 30
m = 30
x = np.linspace(-1, 1, n + 1)
z = np.linspace(-0.1, -1000, m + 1)
x, z = np.meshgrid(x, z)
x = x.ravel()
z = z.ravel()
Let’s store which ones are on the wall and which ones are at the corner for plotting purposes.
on_x_wall = np.abs(x) == 1
on_z_wall = np.logical_or(z == z.min(), z == z.max())
coloring = (0.2 + np.logical_or(on_x_wall, on_z_wall)) / 1.2
corner = np.logical_and(on_x_wall, on_z_wall)
Run the test and plot#
Finally, we can run the simulation, and plot the trajectories.
pt = sd.Particle(
x=x, y=np.zeros_like(x), z=z, t=np.zeros_like(x), data=tub, transport=True
)
Again, we will look at how much the stream function changed before and after the simulation.
kkk = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
gknw = sd.KnW(kkk, vkernel="linear", tkernel="nearest")
before = pt.interpolate("streamfunc", gknw)
steps = 40
stops, ps = pt.to_list_of_time(
normal_stops=np.linspace(0, -2 * steps * N, steps), update_stops=[]
)
1970-01-01T00:00:00
1969-12-31T23:56:35
1969-12-31T23:53:10
1969-12-31T23:49:45
1969-12-31T23:46:19
1969-12-31T23:42:54
1969-12-31T23:39:29
1969-12-31T23:36:04
1969-12-31T23:32:39
1969-12-31T23:29:14
1969-12-31T23:25:49
1969-12-31T23:22:24
1969-12-31T23:18:58
1969-12-31T23:15:33
1969-12-31T23:12:08
1969-12-31T23:08:43
1969-12-31T23:05:18
1969-12-31T23:01:53
1969-12-31T22:58:28
1969-12-31T22:55:03
1969-12-31T22:51:37
1969-12-31T22:48:12
1969-12-31T22:44:47
1969-12-31T22:41:22
1969-12-31T22:37:57
1969-12-31T22:34:32
1969-12-31T22:31:07
1969-12-31T22:27:42
1969-12-31T22:24:16
1969-12-31T22:20:51
1969-12-31T22:17:26
1969-12-31T22:14:01
1969-12-31T22:10:36
1969-12-31T22:07:11
1969-12-31T22:03:46
1969-12-31T22:00:21
1969-12-31T21:56:55
1969-12-31T21:53:30
1969-12-31T21:50:05
1969-12-31T21:46:40
after = pt.interpolate("streamfunc", gknw)
As promised, the difference is indeed very small.
Show code cell source
is_it_close = np.allclose(after, before, atol=1e-7)
max_difference = np.max(np.abs(after - before))
print(f"Is the stream function is conserved? {is_it_close}")
print(f"The maximum difference is {max_difference }")
Is the stream function is conserved? True
The maximum difference is 1.3688851652204903e-07
Show code cell source
lons = []
deps = []
for ppp in ps:
lons.append(ppp.lon)
deps.append(ppp.dep)
lons = np.array(lons)
deps = np.array(deps)
Show code cell source
norm = colors.Normalize(vmin=0.0, vmax=1.0, clip=True)
mapper = cm.ScalarMappable(norm=norm, cmap=cm.binary)
for i in range(len(x)):
if corner[i]:
plt.plot(lons.T[i], deps.T[i], "x-", c="r")
plt.plot(lons.T[i], deps.T[i], c=mapper.to_rgba(coloring[i]))
plt.ylabel("Depth")
plt.xlabel("X")
plt.title("Particle trajectories in a zonal overturning cell")
plt.show()
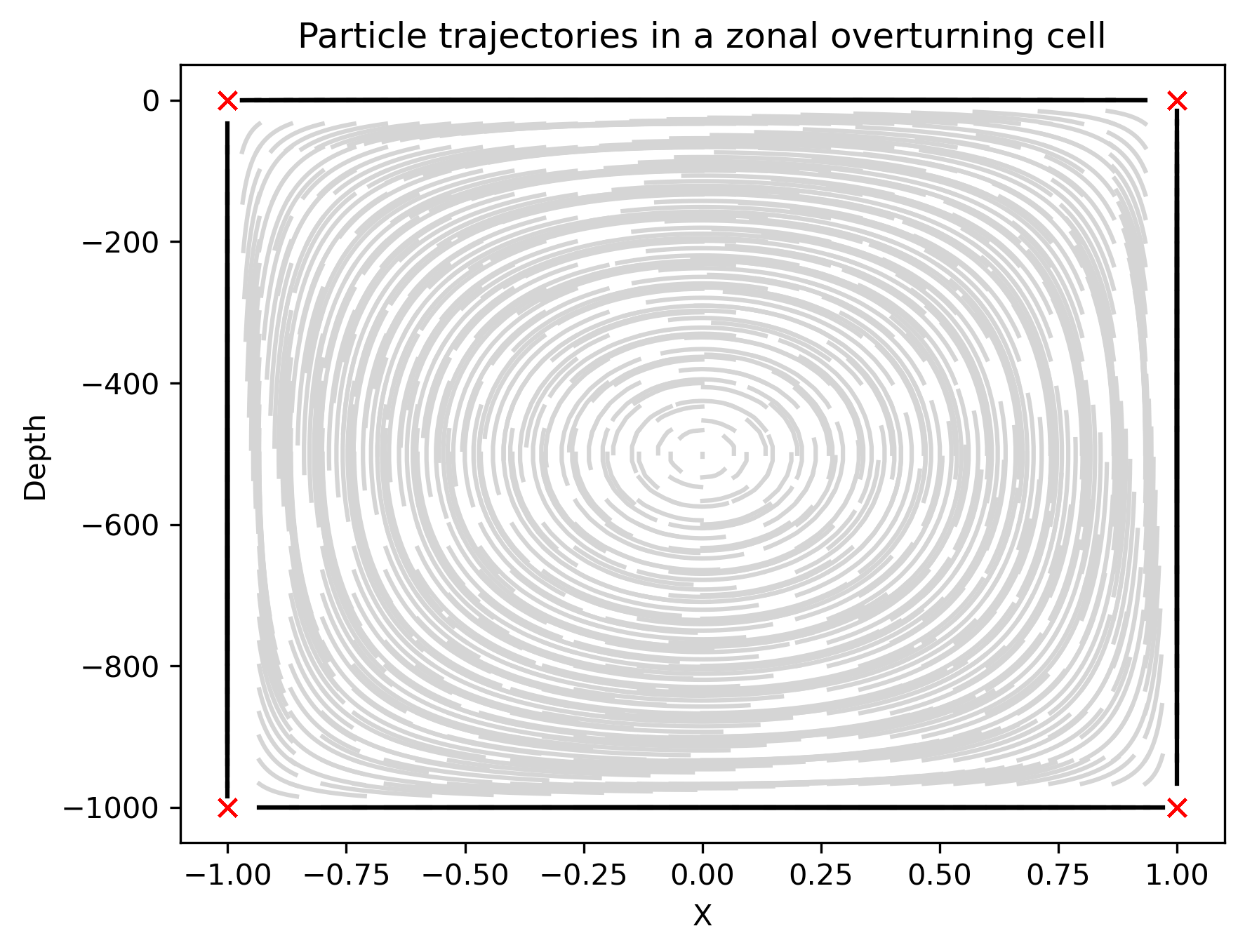
Fig.1 Particle trajectories in zonal overturning cell. Grey and black lines represent the trajectories of interior and wall attached particles, respectively. The red crosses show the trajectories of corner points.
Remarks#
Hopefully, this has already convinced you that the paticles are conserving streamfunction in the vertical.
The non-penetrating condition means that particles on the wall will not detach in any finite time. Likewise, particles at the corners will never leave.
At the center, the point with maximum stream function has nowhere to go, so it stays there forever.